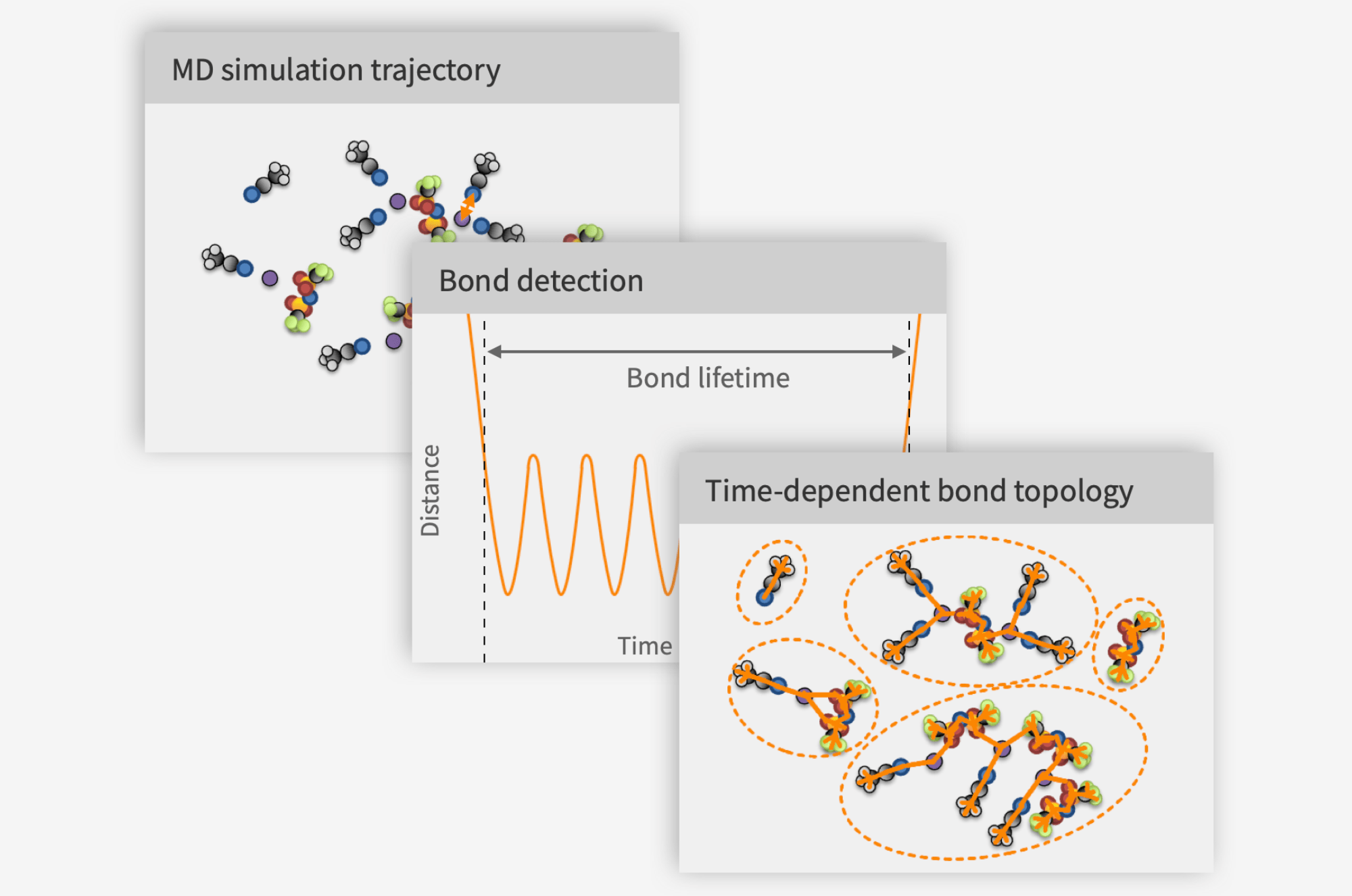
There are many properties that describe transport in electrolytes, but they are not all created equal.
Self-diffusvities are simple
When we talk about diffusivity, what we mean is often self-diffusivity. The self-diffusivity describes how a single species diffuses over time, regardless of how the other components of the electrolyte move at the same time. Computing it is straight-forward – just take the slope of the mean squared displacement curve. You just need to ensure that you have observed the species long enough to enter from the ballistic into the diffusive regime, and that you have gathered enough data to obtain a reasonably straight mean squared displacement curve. In conventional liquid electrolytes, this usually requires a simulation length of around 1 nanosecond.
Take correlations into account
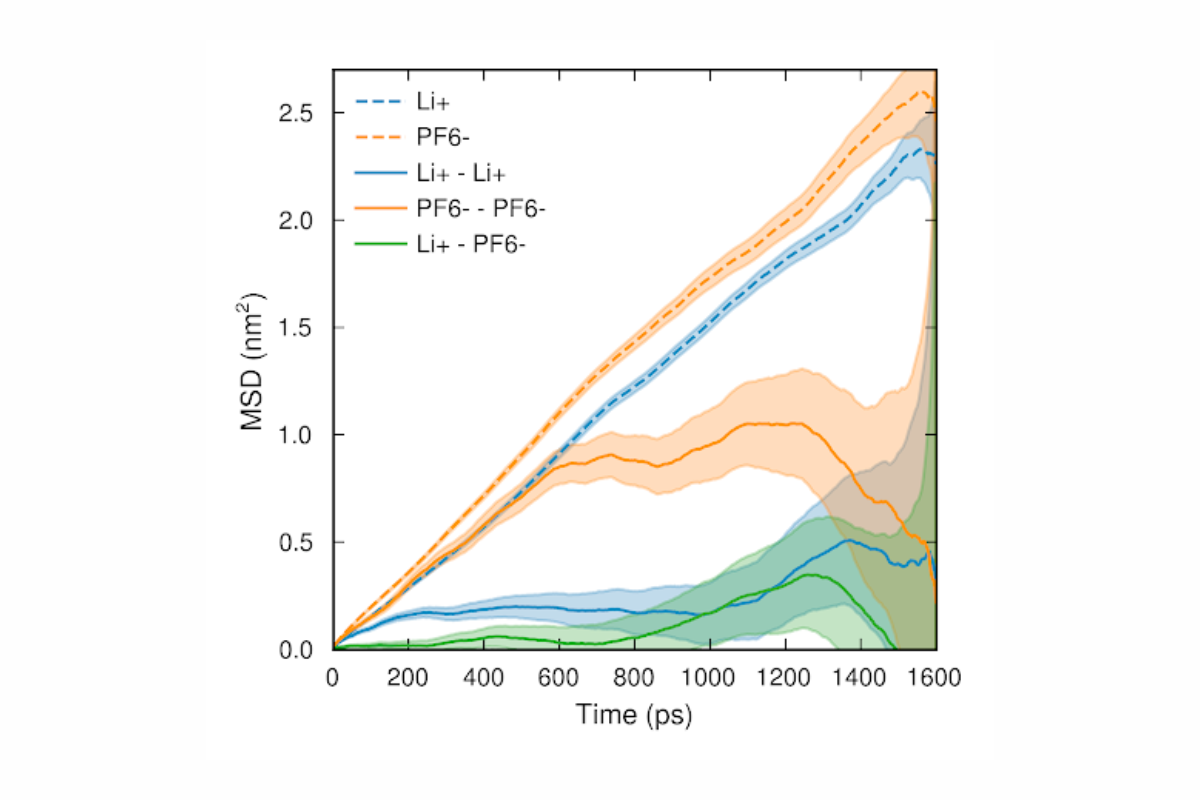
For most transport properties, however, that is not enough. Why? For illustration, we can imagine two extreme cases, either that all cations and anions move in the same direction, or that all cations move in one direction while all anions move in the other. In the former case, the ionic conductivity is zero, whereas in the latter case, it is high. The self-diffusivities do not encode any information that allow us to distinguish between these cases. Predicting the ionic conductivity from self-diffusivities is thus impossible.

Self-diffusivities are simple to compute with relatively little data, Onsager coefficients not so much – if the simulation is too short, it is impossible to measure the slope of the curve.
What do we need to do instead? To predict transport properties, we need to take correlations between ions into account. The conventional approach is to first compute Onsager coefficients, and then transform these into ionic conductivity, salt diffusivity, and transference number. Onsager coefficients can be computed in a fashion very similar to the self-diffusivities, but with a very crucial difference. Instead of taking means over squared displacements of one species at a time, we need to take means over the correlations of the displacements of all pairs of ions. The formulas are similar, but the expressions are a world apart from a numerical standpoint. Most pairs of ions have very little to do with each other, yet all of these pairs will contribute a big dose of noise and very little signal to the final expression. The consequence is that the line that we are supposed to measure the slope of does not become straight until we have run a really long simulation, usually approaching 100 nanoseconds. This is both expensive and time-consuming.
Our solution
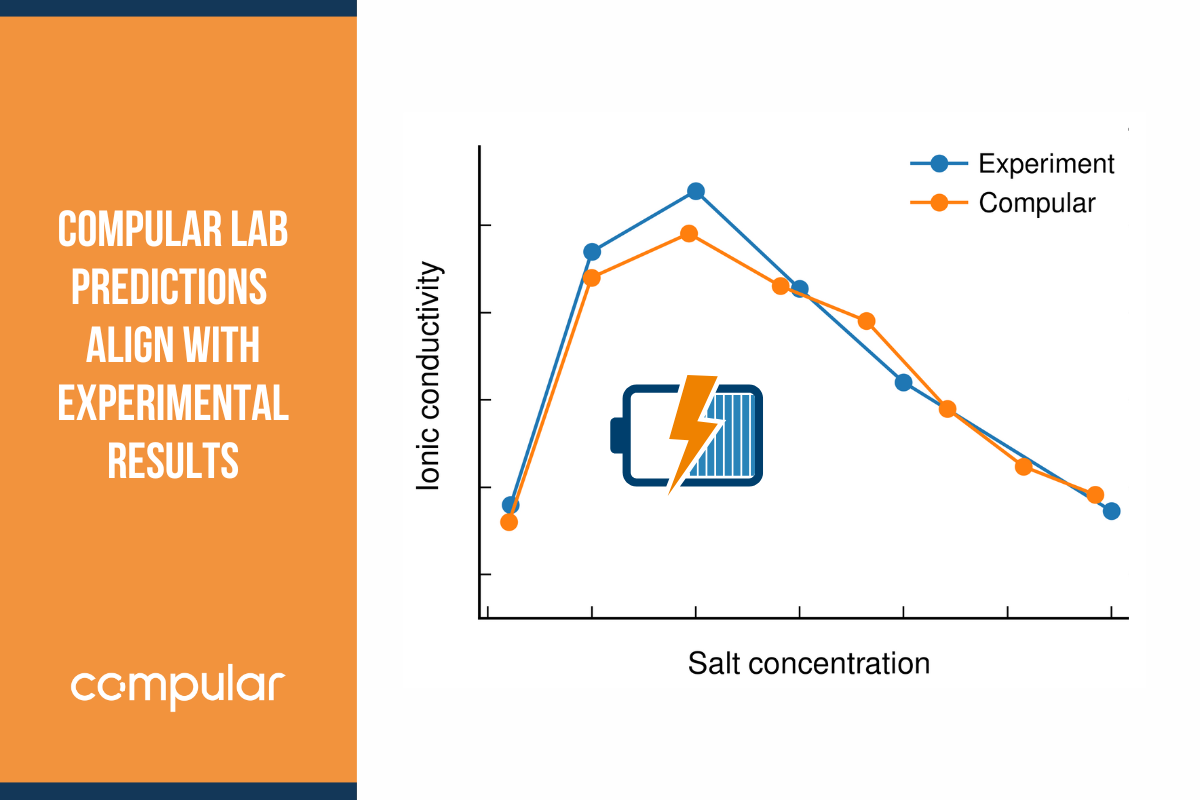
This is where Compular Lab comes to the rescue. Using our patented algorithms, we can make approximations that dramatically reduce the level of noise, slashing the need for data to about a tenth. This suddenly makes molecular dynamics simulations a very cost-efficient tool for uncovering the transport properties of any electrolyte composition. Last week, we released a whitepaper that shows that our approach works for real systems.